分而治之
分而治之算法可以分为三个部分
- 分解原问题为多个子问题(原问题的多个小实例)
- 解决子问题,用返回解决子问题的方式递归算法。递归算法的基本情形可以用来解决子问题
- 组合这些子问题的解决方式,得到原问题的解
二分搜索
上一章中,我们使用迭代的方式实现二分搜索,同样可以用分而治之的方式实现,逻辑如下:
- 分解: 计算 mid 并搜索数组较小或较大的一半
- 解决: 在较小或较大的一半中搜索值
- 合并:这步不需要,我们直接返回索引值
1 | function binarySearchRecursive( |
动态规划
动态规划(dynamic programming, DP)是一种将复杂问题分解成更小的子问题来解决的优化技术。
注意,动态规划和分而治之是不同的方法。分而治之方法是把问题分解成相互独 立的子问题,然后组合它们的答案,而动态规划则是将问题分解成相互依赖的子问题。
用动态规划解决问题时,要遵循三个重要步骤:
- 定义子问题;
- 实现要反复执行来解决子问题的部分;
- 识别并求解出基线条件。
能用动态规划解决的一些著名问题如下:
- 背包问题:给出一组项,各自有值和容量,目标是找出总值最大的项的集合。这个问题 的限制是,总容量必须小于等于“背包”的容量。
- 最长公共子序列:找出一组序列的最长公共子序列(可由另一序列删除元素但不改变余 下元素的顺序而得到)。
- 矩阵链相乘:给出一系列矩阵,目标是找到这些矩阵相乘的最高效办法(计算次数尽可 能少)。相乘运算不会进行,解决方案是找到这些矩阵各自相乘的顺序。
- 硬币找零:给出面额为 d1, …, dn 的一定数量的硬币和要找零的钱数,找出有多少种找零 的方法。
- 图的全源最短路径:对所有顶点对(u, v),找出从顶点 u 到顶点 v 的最短路径。我们在第 9 章已经学习过这个问题的 Floyd-Warshall 算法。
最少硬币找零问题
最少硬币找零问题是硬币找零问题的一个变种。硬币找零问题是给出要找零的钱数,以及可用的硬币面额 d1, …, dn 及其数量,找出有多少种找零方法。最少硬币找零问题是给出要找零的钱 数,以及可用的硬币面额 d1, …, dn 及其数量,找到所需的最少的硬币个数。
例如,美国有以下面额(硬币):d1 = 1,d2 = 5,d3 = 10,d4 = 25。
如果要找 36 美分的零钱,我们可以用 1 个 25 美分、1 个 10 美分和 1 个便士(1 美分)。
如何将这个解答转化成算法?
最少硬币找零的解决方案是找到 n 所需的最小硬币数。但要做到这一点,首先得找到对每个 x < n 的解。然后,我们可以基于更小的值的解来求解。
1 | function minCoinChange(coins, amount) { |
背包问题
背包问题是一个组合优化问题。它可以描述如下:
给定一个固定大小、能够携重量 W 的背 包,以及一组有价值和重量的物品,找出一个最佳解决方案,使得装入背包的物品总重量不超过 W,且总价值最大。
| 物品 | 重量 | 价值 |
|---|---|---|
| 1 | 2 | 3 |
| 2 | 3 | 4 |
| 3 | 4 | 5 |
考虑背包能够携带的重量只有 5。对于这个例子,我们可以说最佳解决方案是往背包里装入 物品 1 和物品 2。这样,总重量为 5,总价值为 7。
这个问题有两个版本。0-1 版本只能往背包里装完整的物品,而分数背包问题则 允许装入分数物品。在这个例子里,我们将处理该问题的 0-1 版本。动态规划对 分数版本无能为力,但本章稍后要学习的贪心算法可以解决它。
1 | function knapSack(capacity, weights, values, n) { |
最长公共子序列
长公共子序列(LCS):
找出两个字符 串序列的最长子序列的长度。最长子序列是指,在两个字符串序列中以相同顺序出现,但不要求 连续(非字符串子串)的字符串序列。
动态规划章节….未完待续
贪心算法
贪心算法遵循一种近似解决问题的技术,期盼通过每个阶段的局部最优选择(当前最好的解),从而达到全局的最优(全局最优解)。
最少硬币找零问题
最少硬币找零问题也能用贪心算法解决。大部分情况下的结果是最优的,不过对有些面额而 言,结果不会是最优的。
1 | function minCoinChange(coins, amount) { |
比起动态规划算法而言,贪心算法更简单、更快。然而,如我们所见,它并不总是得到最优 答案。但是综合来看,它相对执行时间来说,输出了一个可以接受的解。
分数背包问题
在 0-1 背包问题中,只能向背包里装入 完整的物品,而在分数背包问题中,可以装入分数的物品。
| 物品 | 重量 | 价值 |
|---|---|---|
| 1 | 2 | 3 |
| 2 | 3 | 4 |
| 3 | 4 | 5 |
在这种情况下,解决方案是装入物品 1 和物品 2,还有 25%的物品 3。这样,重量为 6 的物 品总价值为 8.25。
1 | function knapSack(capacity, weights, values) { |
回溯算法
回溯是一种渐进式寻找并构建问题解决方式的策略。我们从一个可能的动作开始并试着用这个动作解决问题。如果不能解决,就回溯并选择另一个动作直到将问题解决。根据这种行为,回溯算法会尝试所有可能的动作(如果更快找到了解决办法就尝试较少的次数)来解决问题。
一些可用回溯解决的著名问题:
- 骑士巡逻问题
- N 皇后问题
- 迷宫老鼠问题
- 数独解题器
迷宫老鼠问题
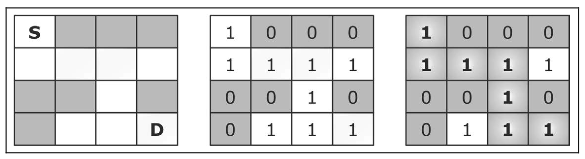
假设我们有一个大小为 N × N 的矩阵,矩阵的每个位置是一个方块。每个位置(或块)可以是空闲的(值为 1)或是被阻挡的(值为 0),如下图所示,其中 S 是起点,D 是终点。
矩阵就是迷宫,“老鼠”的目标是从位置[0][0]开始并移动到[n-1]n-1。老鼠可 以在垂直或水平方向上任何未被阻挡的位置间移动。
解题步骤:
- 创建一个包含解的矩阵。将每个位置初始化为零。对于老鼠采取的每步行动,我们将路径标记为 1。如果算法能够找到一个解,就返回解决矩阵,否则返回一条错误信息
1 | function ratInAMaze(maze) { |
- 我们创建一个 findPath 方法,它会试着从位置 x 和 y 开始在给定的 maze 矩阵中找 到一个解。
1 | function findPath(maze, x, y, solution) { |
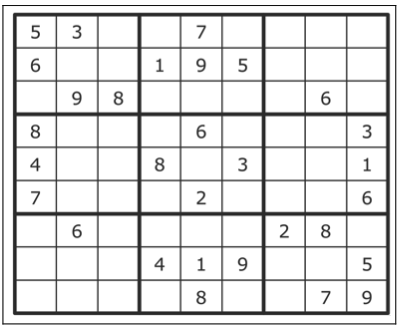
数独解题器
1 | const UNASSIGNED = 0; |