排序算法

我们会从最慢的一个开始，接着是一些性能较好的算法。我们要理解:
首先要学会如何排序，然后再搜索我们需要的信息。

function swap(arr, a, b) {
  // const tmp = array[a];
  // array[a] = array[b];
  // array[b] = tmp;
  [array[a], array[b]] = [array[b], array[a]];
}

冒泡排序

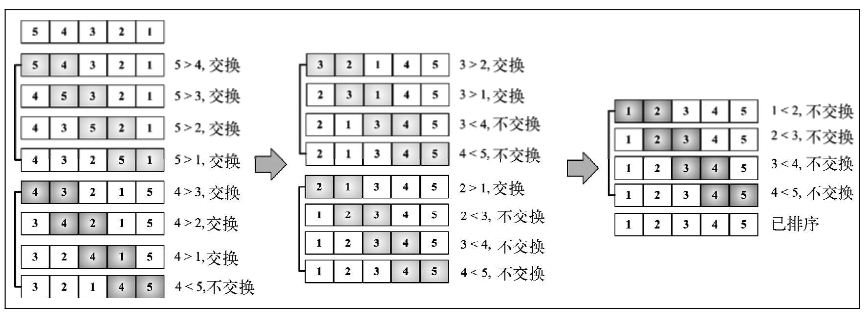
冒泡排序：比较所有相邻的两个项，如果第一个比第二个大，则交换它们。元素项向上移动至正确的顺序，就好像气泡升至表面一样，冒泡排序因此得名

function bubbleSort(array, compareFn = defaultCompare) {
  const { length } = array;
  for (let i = 0; i < length; i++) {
    for (let j = 0; j < length - 1; j++) {
      if (compareFn(array[j], array[j + 1]) === Compare.BIGGER_THAN) {
        swap(array, j, j + 1);
      }
    }
  }
  return array;
}

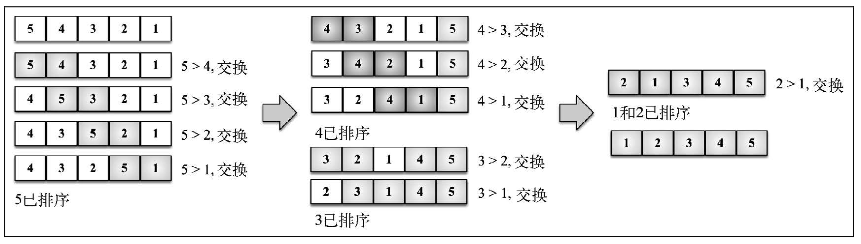
改进后的冒泡排序
如果从内循环减去外循环中已跑过的轮数，就可以避免内循环中所有不必要的比较。

function modifiedBubbleSort(array, compareFn = defaultCompare) {
  const { length } = array;
  for (let i = 0; i < length; i++) {
    for (let j = 0; j < length - 1 - i; j++) {
      if (compareFn(array[j], array[j + 1]) === Compare.BIGGER_THAN) {
        swap(array, j, j + 1);
      }
    }
  }
  return array;
}

复杂度是$O(n^2)$，不推荐。

选择排序

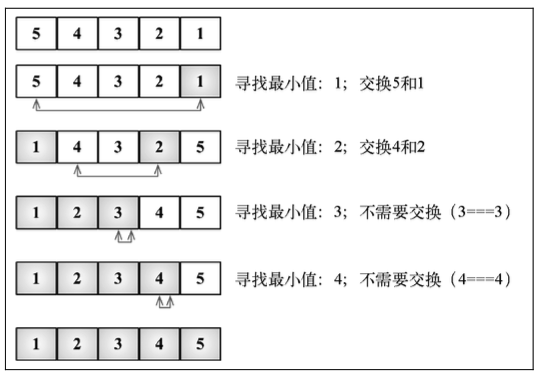
选择排序是一种原址比较排序算法。选择排序大致的思路：找到数据结构中的最小值并将其放置在第一位，接着找到第二小的值并将其放在第二位，以此类推。

function selectionSort(array, compareFn = defaultCompare) {
  const { length } = array;
  let indexMin;
  for (let i = 0; i < length - 1; i++) {
    indexMin = i;
    for (let j = i; j < length; i++) {
      if (compareFn(array[indexMin], array[j]) === Compare.BIGGER_THAN) {
        indexMin = j;
      }
    }
    if (indexMin !== i) {
      swap(array, i, indexMin);
    }
  }
  return array;
}

复杂度是$O(n^2)$，不推荐。

插入排序

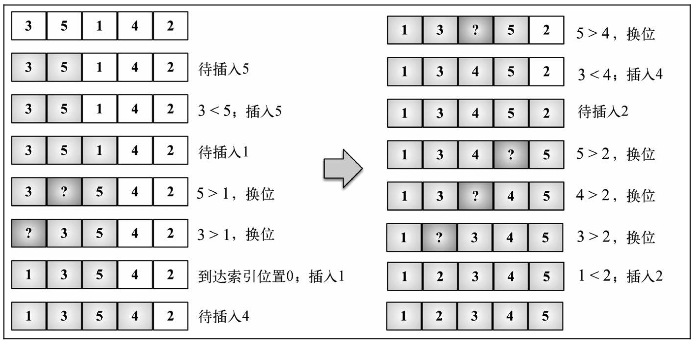
插入排序，每次排一个数组项，以此方式构建最后的排序数组。假定第一项已经排序，接着，它和第二项进行比较，头两项已经正确排序后，接着和第三项比较，以此类推。

function insertionSort(array, compareFn = defaultCompare) {
  const { length } = array;
  let temp;
  for (let i = 1; i < length; i++) {
    let j = i;
    temp = array[i];
    while (j > 0 && compareFn(array[j - 1], temp) === Compare.BIGGER_THAN) {
      array[j] = array[j - 1];
      j--;
    }
    array[j] = temp;
  }
  return array;
}

排序小型数组时，此算法比选择排序和冒泡排序性能要好。

归并排序

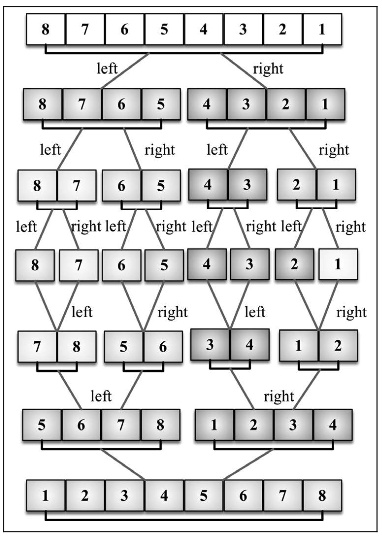
归并排序是一种分而治之算法。其思想是：
将原始数组切分成较小的数组，直到每个小数组只有一个位置，接着将小数组归并成较大的数组，直到最后只有一个排序完毕的大数组。

由于是分治法，归并排序也是递归的。我们要将算法分为两个函数:
第一个负责将一个大数组分为多个小数组并调用用来排序的辅助函数。

function mergeSort(array, compareFn = defaultCompare) {
  if (array.length > 1) {
    const { length } = array;
    const middle = Math.floor(length / 2);
    const left = mergeSort(array.slice(0, middle), compareFn);
    const right = mergeSort(array.slice(middle, length), compareFn);
    array = merge(left, right, compareFn);
  }
  return array;
}

function merge(left, right, compareFn) {
  let i = 0;
  let j = 0;
  let result = [];
  while (i < left.length && j < right.length) {
    result.push(
      compareFn(left[i], right[j]) === Compare.BIGGER_THAN
        ? left[i++]
        : right[j++]
    );
  }
  return result.concat(i < left.length ? left.slice(i) : right.slice(j));
}

快速排序

快速排序，最常用对排序算法，复杂的为 O(nlog(n)),且性能要比其他复杂度为 O(nlog(n))的排序算法好。

快速排序的原理：

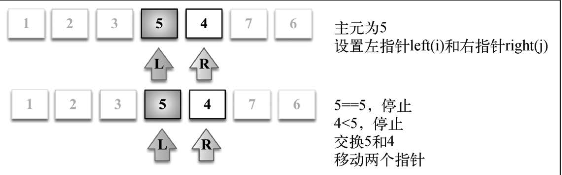
首先，从数组中选择一个值作为主元(pivot)，也就是数组中间的那个值
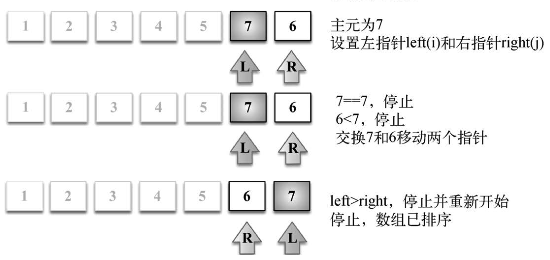
创建两个指针(引用)，左边一个指向数组第一个值，右边一个指向数组最后一个值。移动左指针直到我们找到一个比主元大的值，接着，移动右指针直到找到一个比主元小的值，然后交换它们，重复这个过程，直到左指针超过了右指针。这个过程将使得比主元小的值都排在主元之前，而比主元大的值都排在主元之后。这一步叫作划分(partition)操作。
接着，算法对划分后的小数组(较主元小的值组成的子数组，以及较主元大的值组成的子数组)重复之前的两个步骤，直至数组已完全排序。

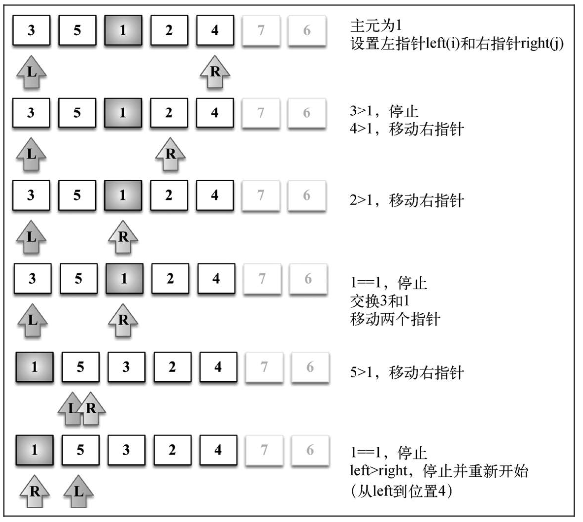
划分操作的第一次执行
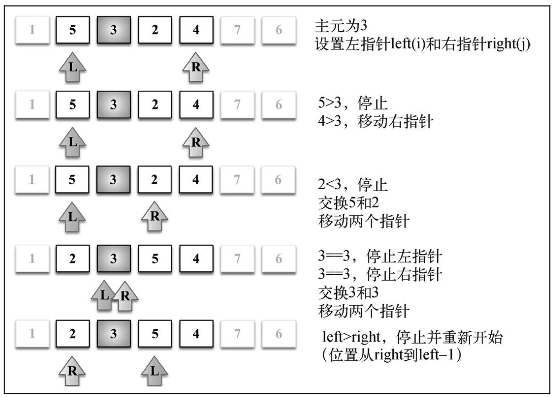
步骤 1 中较小值的子数组执行的划分操作
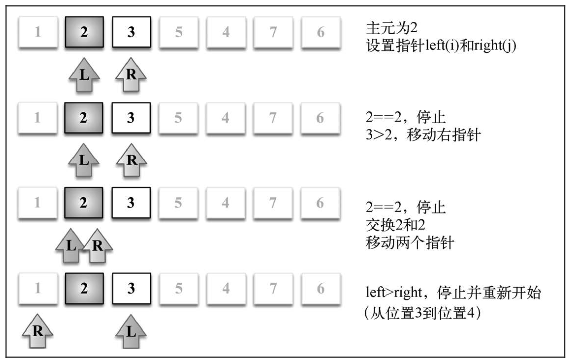
步骤 2 中较大值的子数组执行的划分操作
步骤 3 中较小值的子数组执行的划分操作
步骤 3 中较大值的子数组执行的划分操作
步骤 1 中较大值的子数组执行的划分操作

function quickSort(array, compareFn = defaultCompare) {
  quick(array, 0, array.length - 1, compareFn);
}

function quick(array, left, right, compareFn) {
  let index;
  if (array.length > 1) {
    index = partition(array, left, right, compareFn);
    if (left < index - 1) {
      quick(array, left, index - 1, compareFn);
    }
    if (index < right) {
      quick(array, index, right, compareFn);
    }
  }
  return array;
}

// 划分过程
function partition(array, left, right, compareFn) {
  const pivot = array[Math.floor(left + right) / 2];
  let i = left;
  let j = right;

  while (i <= j) {
    while (compareFn(array[i], pivot) === Compare.LESS_THAN) {
      i++;
    }
    while (compareFn(array[j], pivot) === Compare.BIGGER_THAN) {
      j--;
    }
    if (i <= j) {
      swap(array, i, j);
      i++;
      j--;
    }
  }
  return i;
}

计数排序

分布式排序：使用已组织好的辅助数据结构（称为桶），然后进行合并，得到排好序的数组。
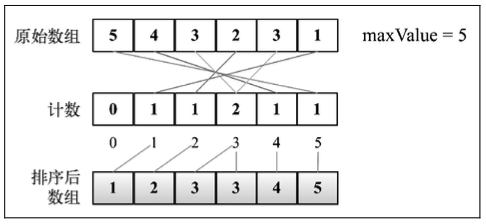
计数排序使用一个用来存储每个元素在原始数组中出现次数的临时数组。在所有元素都计数完成后，临时数组已排好序并可迭代以构建排序后的结果数组。
它是用来排序整数的优秀算法(它是一个整数排序算法)，时间复杂度为 O(n+k)，其中 k 是临时计数数组的大小;但是，它确实需要更多的内存来存放临时数组。

function countingSort(array) {
  if (array.length < 2) {
    return array;
  }

  const maxValue = findMaxValue(array);

  const counts = new Array(maxValue + 1);
  array.forEach((element) => {
    if (!counts[element]) {
      counts[element] = 0;
    }
    counts[element]++;
  });

  let sortedIndex = 0;
  counts.forEach((count, i) => {
    while (count > 0) {
      array[sortedIndex++] = i;
      count--;
    }
  });
  return array;
}

function findMaxValue(array) {
  let max = array[0];
  for (let i = 1; i < array.length; i++) {
    if (array[i] > max) {
      max = array[i];
    }
  }
  return max;
}

桶排序

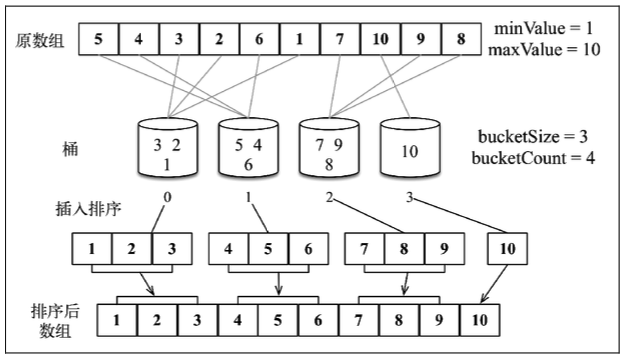
桶排序：(也被称为箱排序)也是分布式排序算法，它将元素分为不同的桶（较小的数组），再使用一个简单的排序算法，例如插入排序(用来排序小数组的不错的算法)，来对每个桶进行排序。然后，它将所有的桶合并为结果数组。

我们将算法分为两个部分:

用于创建桶并将元素分布到不同的桶中，
包含对每个桶执行插入排序算法和将所有桶合并为排序后的结果数组

function bucketSort(array, bucketSize = 5) {
  if (array.length < 2) {
    return array;
  }
  const buckets = createBuckets(array, bucketSize);
  return sortBuckets(buckets);
}

function createBuckets(array, bucketSize) {
  let minValue = array[0];
  let maxValue = array[0];
  for (let i = 1; i < array.length; i++) {
    if (array[i] < minValue) {
      minValue = array[i];
    } else if (array[i] > maxValue) {
      maxValue = array[i];
    }
  }

  const bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;
  const buckets = [];
  for (let i = 0; i < bucketCount; i++) {
    buckets[i] = [];
  }
  for (let i = 0; i < array.length; i++) {
    const bucketIndex = Math.floor((array[i] - minValue) / bucketSize);
    buckets[bucketIndex].push(array[i]);
  }
  return buckets;
}

function sortBuckets(buckets) {
  const sortedArray = [];
  for (let i = 0; i < bucket.length; i++) {
    if (buckets[i] != null) {
      insertionSort(buckets[i]);
      soredArray.push(...buckets[i]);
    }
  }
  return sortedArray;
}

基数排序

待更新

搜索算法

顺序搜索

待更新

二分搜索

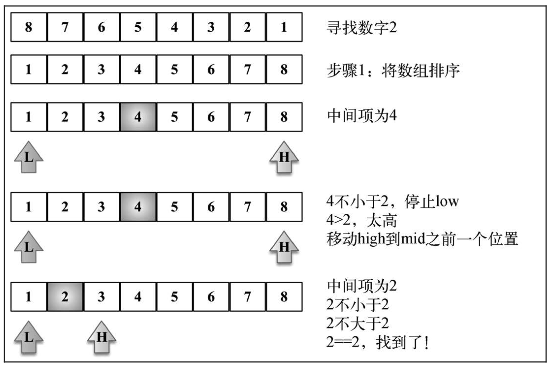
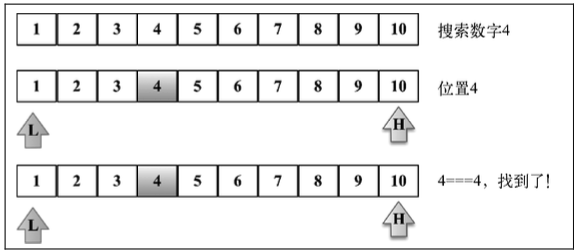
此算法要求被搜索的数据结构已排序。以下是该算法遵循的步骤：

选择数组的中间值
如果选中值是待搜索值，那么算法执行完毕
如果待搜索值比选中值要小，则返回步骤 1 并在选中值左边的子数组中寻找(较小)
如果待搜索值比选中值要大，则返回步骤 1 并在选种值右边的子数组中寻找(较大)

function binarySearch(array, value, compareFn = defaultCompare) {
  const sortedArray = quickSort(array);
  let low = 0;
  let high = sortedArray.length - 1;
  while (
    compareFn(low, hight) === Compare.LESS_THAN ||
    compareFn(low, hight) === Compare.BIGGER_THAN
  ) {
    const mid = Math.floor(low + hight);
    const element = sortedArray[mid];
    if (compareFn(element, value) === Compare.LESS_THAN) {
      low = mid + 1;
    } else if (compareFn(elemnt, value) === Compare.BIGGER_THAN) {
      high = mid - 1;
    } else {
      return mid;
    }
  }
  return DOES_NOT_EXIST;
}

内插搜索

内插搜索是改良版的二分搜索。二分搜索总是检查 mid 位置上的值，而内插搜索可能会根据要搜索的值检查数组中的不同地方。
这个算法要求被搜索的数据结构已排序。以下是该算法遵循的步骤:

使用 position 公式选中一个值;
如果这个值是待搜索值，那么算法执行完毕(值找到了);
如果待搜索值比选中值要小，则返回步骤 1 并在选中值左边的子数组中寻找(较小);
如果待搜索值比选中值要大，则返回步骤 1 并在选种值右边的子数组中寻找(较大)。

function interpolationSearch(
  array,
  value,
  compareFn = defaultCompare,
  equalsFn = defaultEquals,
  diffFn = defaultDiff
) {
  const { length } = array;
  let low = 0;
  let high = length - 1;
  let position = -1;
  let delta = -1;
  while (
    low <= high &&
    biggerOrEquals(value, array[low], compareFn) &&
    lesserOrEquals(value, array[high], compareFn)
  ) {
    delta = diffFn(value, array[low]) / diffFn(array[high], array[low]);
    position = low + Math.floor((high - low) * delta);
    if (equalsFn(array[position], value)) {
      return position;
    }
    if (compareFn(array[position], value) === Compare.LESS_THAN) {
      low = position + 1;
    } else {
      high = position - 1;
    }
  }
  return DOES_NOT_EXIST;
}

function lesserOrEquals(a, b, compareFn) {
  const comp = compareFn(a, b);
  return comp === Compare.LESS_THAN || comp === Compare.EQUALS;
}
function biggerOrEquals(a, b, compareFn) {
  const comp = compareFn(a, b);
  return comp === Compare.BIGGER_THAN || comp === Compare.EQUALS;
}

随机算法

Fisher-Yates随机

它的含义是迭代数组，从最后一位开始并将当前位置和一个随机位置进行交换。这个随机位置比当前位置小。这样，这个算法可以保证随机过的位置不会再被随机一次(洗扑克牌的次数越多，随机效果越差)。

function shuffle(array) {
  for(let i = array.length - 1 ; i > 0 ;i--) {
    const randomIndex = Math.floor(Math.random() * (i + 1))
    swap(array, i, randomIndex)
  }
  return array
}

Stay hungry. Stay foolish.

javascript数据结构与算法8