图的相关术语

图是一组由边连接的节点(或顶点)。
任何社交网络、道路、通信、航班都能用图来表示。
一个图 G = (V, E)由以下元素组成。

V:一组顶点
E:一组边，连接 V 中的顶点

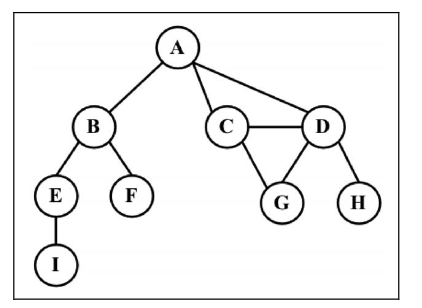
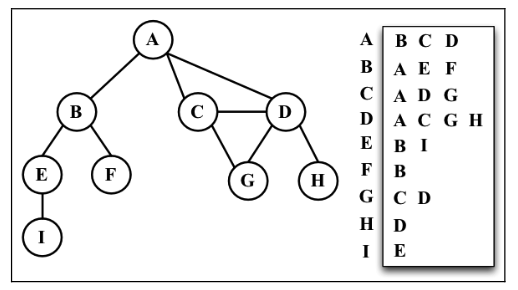
由一条边连接在一起的顶点称为相邻顶点。比如，A 和 B 是相邻的，A 和 D 是相邻的，A 和 C 是相邻的，A 和 E 不是相邻的。
一个顶点的度是其相邻顶点的数量。比如，A 和其他三个顶点相连接，因此 A 的度为 3;E 和其他两个顶点相连，因此 E 的度为 2。
路径是顶点 v1, v2, …, vk 的一个连续序列，其中 vi 和 vi+1 是相邻的。以上一示意图中的图为例，其中包含路径 A B E I 和 A C D G。
简单路径要求不包含重复的顶点。举个例子，A D G 是一条简单路径。除去最后一个顶点(因为它和第一个顶点是同一个顶点)，环也是一个简单路径，比如 A D C A(最后一个顶点重新回到 A)。
如果图中不存在环，则称该图是无环的。如果图中每两个顶点间都存在路径，则该图是连通的。

有向图和无向图
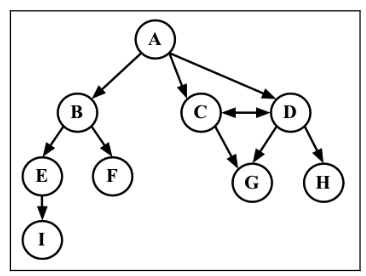
图可以是无向的(边没有方向)或是有向的(有向图)。如下图所示，有向图的边有一个方向。

如果图中每两个顶点间在双向上都存在路径，则该图是强连通的。例如，C 和 D 是强连通的，而 A 和 B 不是强连通的。

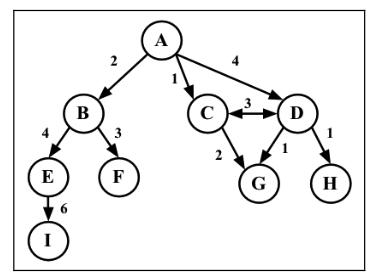
图还可以是未加权的(目前为止我们看到的图都是未加权的)或是加权的。如下图所示，加权图的边被赋予了权值。

图的表示

从数据结构的角度来说，我们有多种方式来表示图。在所有的表示法中，不存在绝对正确的方式。图的正确表示法取决于待解决的问题和图的类型。

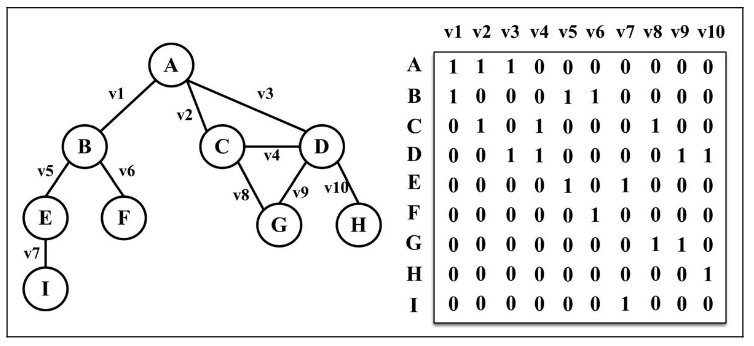
邻接矩阵

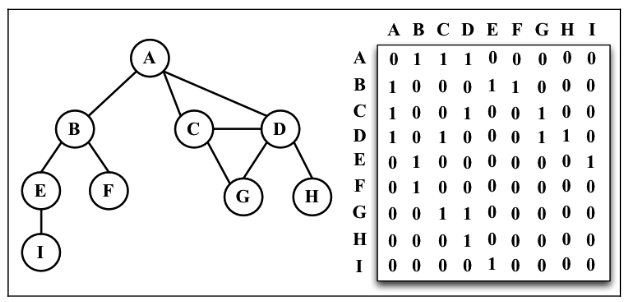
图最常见的实现是邻接矩阵。每个节点都和一个整数相关联，该整数将作为数组的索引。我们用一个二维数组来表示顶点之间的连接。如果索引为 i 的节点和索引为 j 的节点相邻，则 array[i][j] === 1，否则 array[i][j] === 0，如下图所示。

邻接表

邻接表，一种动态数据结构来表示图。邻接表由图中每个顶点的相邻顶点列表所组成。存在好几种方式来表示这种数据结构。我们可以用列表(数组)、链表，甚至是散列表或是字典来表示相邻顶点列表。下面的示意图展示了邻接表数据结构。

尽管邻接表可能对大多数问题来说都是更好的选择，但以上两种表示法都很有用，且它们有着不同的性质(例如，要找出顶点 v 和 w 是否相邻，使用邻接矩阵会比较快)。在本书的示例中，我们将会使用邻接表表示法

关联矩阵

在关联矩阵中，矩阵的行表示顶点，列表示边。如下图所示，使用二维数组来表示两者之间的连通性，如果顶点 v 是边 e 的入射点，则 array[v][e] === 1; 否则，array[v][e] === 0。

关联矩阵通常用于边的数量比顶点多的情况，以节省空间和内存。

创建 Graph 类

Graph 构造函数可以接收一个参数来表示图是否有向，默认情况下，图是无向的。用一个数组来存储图中所有顶点的名字，以及一个字典来存储邻接表。字典将会使用顶点的名字作为键，邻接顶点列表作为值。

class Graph {
  constructor(isDirected = false) {
    this.isDirected = isDirected;
    this.vertices = [];
    this.adjList = new Dictionary();
  }

  addVertex() {
    if (!this.vertices.includes(v)) {
      this.vertices.push(v);
      this.adjList.set(v, []);
    }
  }

  addEdge(v, w) {
    if (!this.adjList.get(v)) {
      this.addVertex(v);
    }

    if (!this.adjList.get(w)) {
      this.addVertex(w);
    }

    this.adjList.get(v).push(w);
    if (!this.isDirected) {
      this.adjList.get(w).push(v);
    }
  }

  getVertices() {
    return this.vertices;
  }

  getAdjList() {
    return this.adjList;
  }
}

图的遍历

有两种算法可以对图进行遍历:
广度优先搜索(breadth-first search，BFS)和深度优先搜索(depth-first search，DFS)。
图遍历可以用来寻找特定的顶点或寻找两个顶点之间的路径，检查图是否连通，检查图是否含有环，等等。

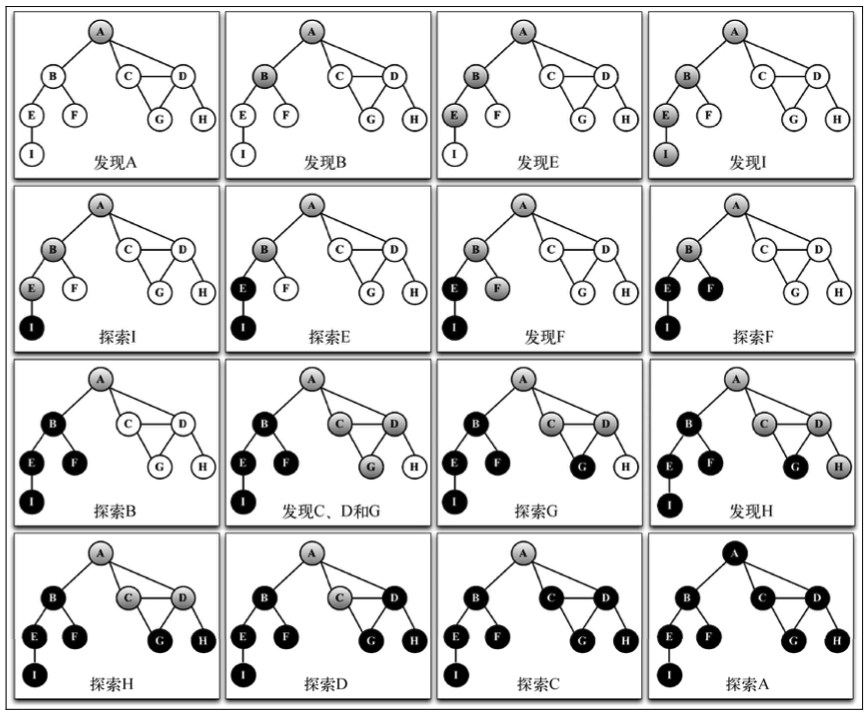
图遍历算法的思想是必须追踪每个第一次访问的节点，并且追踪有哪些节点还没有被完全探索。对于两种图遍历算法，都需要明确指出第一个被访问的顶点。

完全探索一个顶点要求我们查看该顶点的每一条边。对于每一条边所连接的没有被访问过的顶点，将其标注为被发现的，并将其加进待访问顶点列表中。

广度优先搜索算法和深度优先搜索算法基本上是相同的，只有一点不同，那就是待访问顶点列表的数据结构，如下表所示。
算法 | 数据结构 | 描述
—|—|—
深度优先 | 栈 | 将顶点存入栈，顶点是沿着路径被探索的，存在新的相邻顶点就去访问
广度优先 | 队列 | 将顶点存入队列，最先入队列的顶点被探索

当要标注已经访问过的顶点时，我们用三种颜色来反映它们的状态。

白色:表示该顶点还没有被访问。
灰色:表示该顶点被访问过，但并未被探索过。
黑色:表示该顶点被访问过且被完全探索过

两个算法还需要一个辅助对象来帮助存储顶点是否被访问过。在每个算法的开头，所有的顶点会被标记为未访问(白色)。我们要用下面的函数来初始化每个顶点的颜色。

const Colors = {
  WHITE: 0,
  GREY: 1,
  BLACK: 2
};

function initializeColor = vertices => {
  const color = {}
  for(let i = 0; i < vertices.length; i++) {
    color[vertices[i]] = Colors.WHITE
  }
  return color
}

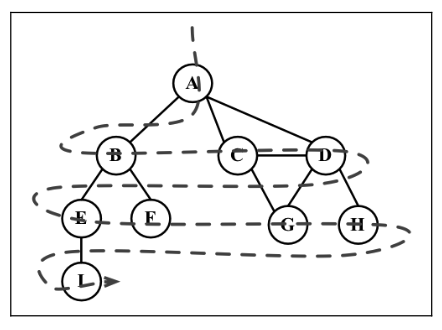
广度优先搜索

广度优先搜索算法会从指定的第一个顶点开始遍历图，先访问其所有的邻点(相邻顶点)，就像一次访问图的一层。换句话说，就是先宽后深地访问顶点，如下图所示：

以下是从顶点 v 开始的广度优先搜索算法所遵循的步骤。

创建一个队列 Q。
标注 v 为被发现的(灰色)，并将 v 入队列 Q。如果 Q 非空，则运行以下步骤:
将 u 从 Q 中出队列;
标注 u 为被发现的(灰色);
将 u 所有未被访问过的邻点(白色)入队列;标注 u 为已被探索的(黑色)。

const breathFirstSearch = (graph, startVertex, callback) => {
  const vertices = graph.getVertices();
  const adjList = graph.getAdjList();
  const color = initializeColor(vertices);

  const queue = new Queue();

  queue.enqueue(startVertex);

  while (!queue.isEmpty()) {
    const u = queue.dequeue();
    const neighbors = adjList.get(u);
    color[u] = Colors.GREY;
    for (let i = 0; i < neighbors.length; i++) {
      const w = neighbors[i];
      if (color[w] === Colors.WHITE) {
        color[w] = Colors.GREY;
        queue.enqueue(w);
      }
    }
    color[u] = Color.BLACK;
    if (callback) {
      callback(u);
    }
  }
};

1.使用 BFS 寻找最短路径

考虑如何解决下面问题：

给定一个图 G 和源顶点 v，找出每个顶点 u 和 v 之间最短路径的距离(以边的数量计)。

对于给定顶点 v，广度优先算法会访问所有与其距离为 1 的顶点，接着是距离为 2 的顶点，以此类推。所以，可以用广度优先算法来解这个问题。我们可以修改 breadthFirstSearch 方法以返回给我们一些信息

从 v 到 u 的距离
前溯点 predecessors[u]，用来推导出从 v 到其他每个顶点 u 的最短路径

// 改进后的广度优先方法
const BFS = (graph, startVertex) => {
  const vertices = graph.getVertices();
  const adjList = graph.getAdjList();
  const color = initializeColor(vertices);
  const queue = new Queue();
  const distances = {};
  const predecessors = {};
  queue.enqueue(startVertex);

  for (let i = 0; i < vertices.length; i++) {
    distances[vertices[i]] = 0;
    predecessors[vertices[i]] = null;
  }

  while (!queue.isEmpty()) {
    const u = queue.dequeue();
    const neighbors = adjList.get(u);
    color[u] = Colors.GREY;
    for (let i = 0; i < neighbors.length; i++) {
      const w = neighbors[i];
      if ((color[w] = Colors.WHITE)) {
        color[w] = Colors.GREY;
        distances[w] = distances[u] + 1;
        predecessors[w] = u;
        queue.enqueue(w);
      }
    }
    color[u] = Colors.BLACK;
  }

  return {
    distance,
    predecessors,
  };
};
const myVertices = ["A", "B", "C", "D", "E", "F", "G", "H", "I"];
const shortestPathA = BFS(graph, myVertices[0]);

// distances: [A: 0, B: 1, C: 1, D: 1, E: 2, F: 2, G: 2, H: 2 , I: 3],
// predecessors: [A: null, B: "A", C: "A", D: "A", E: "B", F: "B", G: "C", H: "D", I: "E"]

通过前溯点数组，我们可以用下面这段代码来构建从顶点 A 到其他顶点的路径

const fromVertex = myVertices[0];

for (let i = 0; i < myVertices.length; i++) {
  const toVertex = myVertices[i];
  const path = new Stack();
  for (let v = toVertex; v !== fromVertex; v = shortestPathA.predecessors(v)) {
    path.push(v);
  }
  path.push(fromVertex);
  let s = path.pop();
  while (!path.isEmpty()) {
    s += " - " + path.pop();
  }
  consloe.log(s);
}

2.深入学校最短路径算法

本章中的图不是加权图。如果要计算加权图中的最短路径(例如，城市 A 和城市 B 之间的最短路径——GPS 和 Google Maps 中用到的算法)，广度优先搜索未必合适。

举几个例子，Dijkstra 算法解决了单源最短路径问题。Bellman-Ford 算法解决了边权值为负的单源最短路径问题。A*搜索算法解决了求仅一对顶点间的最短路径问题，用经验法则来加速搜索过程。Floyd-Warshall 算法解决了求所有顶点对之间的最短路径这一问题。

我们会在本章后面学习 Dijkstra 算法和 Floyd-Warshall 算法。

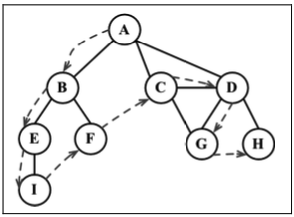
深度优先搜索

深度优先搜索算法将会从第一个指定的顶点开始遍历图，沿着路径直到这条路径最后一个顶点被访问了，接着原路回退并探索下一条路径。换句话说，它是先深度后广度地访问顶点，如下图所示。

深度优先搜索算法不需要一个源顶点。在深度优先搜索算法中，若图中顶点 v 未访问，则访问该顶点 v。
要访问顶点 v，照如下步骤做:

标注 v 为被发现的(灰色);
对于 v 的所有未访问(白色)的邻点 w，访问顶点 w;
标注 v 为已被探索的(黑色)。
深度优先搜索的步骤是递归的，这意味着深度优先搜索算法使用栈来存储函数调用(由递归调用所创建的栈)。

const depthFirstSearch = (graph, callback) => {
  const vertices = graph.getVertices();
  const adjList = graph.getAdjList();
  const color = initializeColor(vertices);

  for (let i = 0; i < vertices.length; i++) {
    if (color[vertices[i]] === Colors.WHITE) {
      depthFirstSearchVisit(vertices[i], color, adjList, callback);
    }
  }

  const depthFirstSearchVisit = (u, color, adjList, callback) => {
    color[u] = Colors.GREY;
    if (callback) {
      callback(u);
    }
    const neighbors = adjList.get(u);
    for (let i = 0; i < neighbors.length; i++) {
      const w = neighbors[i];
      if (color[w] === Colors.WHITE) {
        depthFirstSearchVisit(w, color, adjList, callback);
      }
    }
    color[u] = Colors.BLACK;
  };
};

下面这个示意图展示了该算法每一步的执行过程:

1. 探索深度优先算法

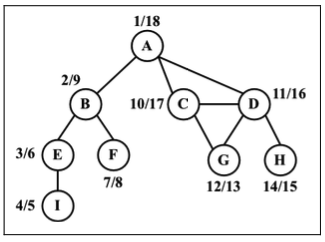
对于给定的图 G，我们希望深度优先搜索算法遍历图 G 的所有节点，构建“森林”(有根树的一个集合)以及一组源顶点(根)，并输出两个数组:发现时间和完成探索时间。我们可以修改 depthFirstSearch 函数来返回一些信息：

顶点 u 的发现时间 d[u]
当顶点 u 被标注为黑色时，u 的完成探索时间 f[u]
顶点 u 的前溯点 p[u]

const DFS = (graph) => {
  const vertices = graph.getVertices();
  const adjList = graph.getAdjList();
  const color = initializeColor(vertices);
  const d = {};
  const f = {};
  const p = {};
  const time = { count: 0 };
  for (let i = 0; i < vertices.length; i++) {
    f[vertices[i]] = 0;
    d[vertices[i]] = 0;
    p[vertices[i]] = null;
  }

  for (let i = 0; i < vertices.length; i++) {
    if (color[vertices[i]] === Colors.WHITE) {
      DFSVisit(vertices[i], color, d, f, p, time, adjList);
    }
  }

  return {
    discovery: d,
    finished: f,
    predecessors: p,
  };
};

const DFSVisit = (u, color, d, f, p, time, adjList) => {
  color[u] = Colors.GREY;
  d[u] = ++time.count;
  const neighbors = adjList.get(u);
  for (let i = 0; i < neighbors.length; i++) {
    const w = neighbors[i];
    if (color[w] === Colors.WHITE) {
      p[w] = u;
      DFSVisit(w, color, d, f, p, time, adjList);
    }
  }
  color[u] = Colors.BLACK;
  f[u] = ++time.count;
};

深度优先算法背后的思想是什么?

边是从最近发现的顶点 u 处被向外探索的。只有连接到未发现的顶点的边被探索了。当 u 所有的边都被探索了，该算法回退到 u 被发现的地方去探索其他的边。这个过程持续到我们发现了所有从原始顶点能够触及的顶点。如果还留有任何其他未被发现的顶点，我们对新源顶点重复这个过程。重复该算法，直到图中所有的顶点都被探索了。

对于改进过的深度优先搜索，有两点需要我们注意:

时间(time)变量值的范围只可能在图顶点数量的一倍到两倍(2|V|)之间;
对于所有的顶点 u，d[u]<fu。

在这两个假设下，我们有如下的规则。

1 <= d [u] < f [u] <= 2|V|

如果对同一个图再跑一遍新的深度优先搜索方法，对图中每个顶点，我们会得到如下的发现/完成时间。

2. 拓扑排序——使用深度优先搜索

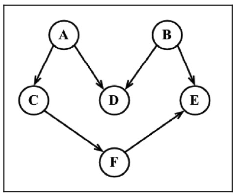
给定下图，假定每个顶点都是一个我们需要去执行的任务。

这是一个有向图，意味着任务的执行是有顺序的。例如，任务 F 不能在任务 A 之前执行。注意这个图没有环，意味着这是一个无环图。所以，我们可以说该图是一个有向无环图(DAG)。

当我们需要编排一些任务或步骤的执行顺序时，这称为拓扑排序(topological sorting，英文亦写作 topsort 或是 toposort)。

拓扑排序只能应用于 DAG。

graph = new Graph(true); // 有向图

myVertices = ["A", "B", "C", "D", "E", "F"];
for (i = 0; i < myVertices.length; i++) {
  graph.addVertex(myVertices[i]);
}

graph.addEdge("A", "C");
graph.addEdge("A", "D");
graph.addEdge("B", "D");
graph.addEdge("B", "E");
graph.addEdge("C", "F");
graph.addEdge("F", "E");

const result = DFS(graph);

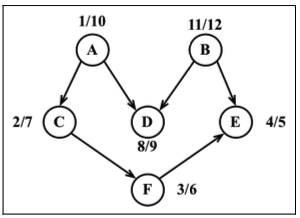
以倒序来排序完成时间数组，这便得出了该图的拓扑排序，如下所示

const fTimes = result.finished;
s = "";
for (let i = 0; i < myVertices.length; i++) {
  let max = 0;
  let maxName = null;
  if (fTimes[myVertices[i]] > max) {
    max = fTimes[myVertices[i]];
    maxName = myVertices[i];
  }
  s += " - " + maxName;
  delete fTimes[maxName];
}
console.log(s);

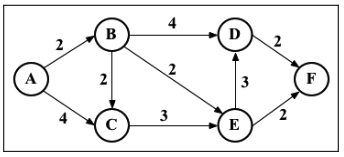
最短路径算法

Dijkstra 算法和 Floyd-Warshall 算法

Dijkstra 算法

Dijkstra 算法是一种计算从单个源到所有其他源的最短路径的贪心算法，这意味着我们可以用它来计算从图的一个顶点到其余各顶点的最短路径。

// 上图的邻接矩阵
var graph = [
  [0, 2, 4, 0, 0, 0],
  [0, 0, 2, 4, 2, 0],
  [0, 0, 0, 0, 3, 0],
  [0, 0, 0, 0, 0, 2],
  [0, 0, 0, 3, 0, 2],
  [0, 0, 0, 0, 0, 0],
];

const minDistance = (dist, visited) => {
  let min = INF;
  let minIndex = -1;
  for (let v = 0; v < visited.length; v++) {
    if (visited[v] === false && dist[v] <= min) {
      min = dist[v];
      minIndex = v;
    }
  }
  return minIndex;
};

// Dijkstra算法
const INF = Number.MAX_SAFE_INTEGER;

const dijkstra = (graph, src) => {
  const dist = [];
  const visited = [];
  const { length } = graph;
  for (let i = 0; i < length; i++) {
    dist[i] = INF;
    visited[i] = false;
  }
  dist[src] = 0;
  for (let i = 0; i < length - 1; i++) {
    const u = minDistance(dist, visited);
    visited[u] = true;
    for (let v = 0; v < length; v++) {
      if (
        !visited[v] &&
        graph[u][v] !== 0 &&
        dist[u] != INF &&
        dist[u] + graph[u][v] < dist[v]
      ) {
        dist[v] = dist[u] + graph[u][v];
      }
    }
  }
  return dist;
};

Floyd-Warshall 算法

Floyd-Warshall 算法是一种计算图中所有最短路径的动态规划算法。通过该算法，我们可以找出从所有源到所有顶点的最短路径。

const floyWarshall = graph => {
  const dist = []
  const {length} = graph
  for(let i = 0; i < length; i++) {
    dist[i] = []
    for(let j = 0; j < length; j++) {
      if(i === j) {
        dist[i][j] = 0
      } else if(!isFinite(graph[i][j])) {
        dist[i][j] = Infinity
      } else {
        dist[i][j] = graph[i][j]
      }
    }
  }

  for(let k = 0; k < length; k++) {
    for(let i = 0; i < length; i++) {
      for(let j = 0; j < length; j++) {
        if(dist[i][k] + dist[k][j] < dist[i][j]) {
          dist[i][j] = dist[i][k] + dist[k][j]
        }
      }
    }
  }
  return dists
}

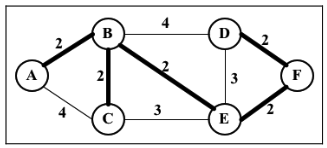
最小生成树

最小生成树(MST)问题是网络设计中常见的问题。想象一下，你的公司有几间办公室，要以最低的成本实现办公室电话线路相互连通，以节省资金，最好的办法是什么?

这也可以应用于岛桥问题。设想你要在 n 个岛屿之间建造桥梁，想用最低的成本实现所有岛屿相互连通。

这两个问题都可以用 MST 算法来解决，其中的办公室或者岛屿可以表示为图中的一个顶点，边代表成本。下面有一个图的例子，其中较粗的边是一个 MST 的解决方案。

两种主要的求最小生成树的算法：Prim算法和kruskal算法

Prim算法

Prim 算法是一种求解加权无向连通图的 MST 问题的贪心算法。它能找出一个边的子集，使得其构成的树包含图中所有顶点，且边的权值之和最小。

const INF = Number.MAX_SAFE_INTEGER

const minKey = (graph, key, visited) => {
  // Initialize min value
  let min = INF;
  let minIndex = 0;
  for (let v = 0; v < graph.length; v++) {
    if (visited[v] === false && key[v] < min) {
      min = key[v];
      minIndex = v;
    }
  }
  return minIndex;
};

const prim = graph => {
  const parent = []
  const key = []
  const visited = []
  const {length} = graph
  for(let i = 0; i < length; i++) {
    key[i] = INF
    visited[i] = false
  }
  key[0] = 0
  parent[0] = -1
  for(let i = 0; i < length - 1; i++) {
    const u = minKey(graph, key, visited)
    visited[u] = true
    for(let v = 0; v < length; v++) {
      if(graph[u][v] && !visited[v] && graph[u][v] < key[v]) {
        parent[v] = u
        key[v] = graph[u][v]
      }
    }
  }
  return parent
}

Kruskal 算法

也是一种求加权无向连通图的MST的贪心算法

const INF = Number.MAX_SAFE_INTEGER;

const find = (i, parent) => {
  while (parent[i]) {
    i = parent[i]; 
  }
  return i;
};

const union = (i, j, parent) => {
  if (i !== j) {
    parent[j] = i;
    return true;
  }
  return false;
};

const initializeCost = graph => {
  const cost = [];
  const { length } = graph;
  for (let i = 0; i < length; i++) {
    cost[i] = [];
    for (let j = 0; j < length; j++) {
      if (graph[i][j] === 0) {
        cost[i][j] = INF;
      } else {
        cost[i][j] = graph[i][j];
      }
    }
  }
  return cost;
};

const kruskal = graph => {
  const {length} = graph
  const parent = []
  let ne = 0
  let a;let b; let u;let v;
  const cost = initializeCost(graph)
  while(ne < length - 1) {
    for(let i = 0,min = INF; i < length; i++) {
      for(let j = 0; j < length; j++) {
        if(cost[i][j] < min) {
          min = cost[i][j]
          a = u =i
          b = u =j
        }
      }
    }
    u = find(u, parent)
    v = find(v, parent)
    if(union(u,vparent)) {
      ne++
    }
    cost[a][b] = cost[b][a] = INF
  }
  return parent
}

Stay hungry. Stay foolish.

javascript数据结构与算法7