javascript数据结构与算法5

发表于
树，存储需要快速查找的数据的非顺序数据结构

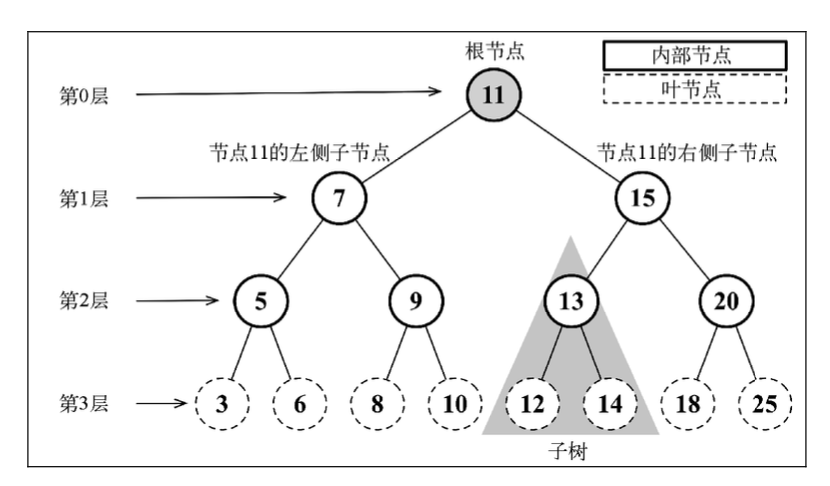
树的相关术语

二叉树和二叉搜索树

二叉树中的节点最多只能有两个子节点:一个是左侧子节点，另一个是右侧子节点。
二叉搜索树(BST)是二叉树的一种，但是只允许你在左侧节点存储(比父节点)小的值， 在右侧节点存储(比父节点)大的值。

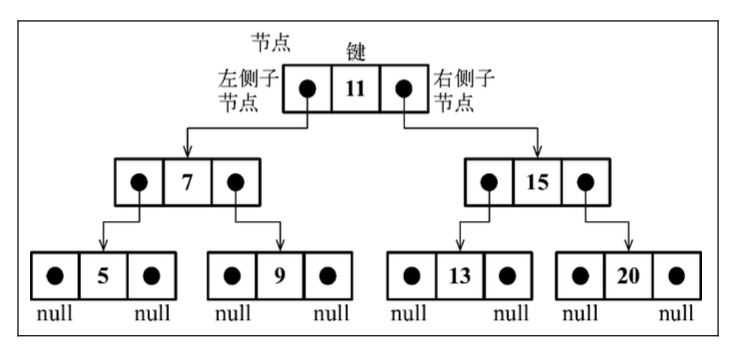
创建 BinarySearchTree 类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Node {
  constructor(key) {
    this.key = key;
    this.left = null;
    this.right = null;
  }
}

class BinarySearchTree extends Node {
  constructor(compareFn = defaultCompare) {
    this.compareFn = compareFn;
    this.root = null;
  }

  insert(key) {
    if (this.root == null) {
      this.root = new Node(key);
    } else {
      this.insertNode(this.root, key);
    }
  }

  insertNode(node, key) {
    if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
      if (node.left == null) {
        node.left = new Node(key);
      } else {
        this.insertNode(node.left, key);
      }
    } else {
      if (node.right == null) {
        node.right = new Node(key);
      } else {
        this.insertNode(node.right, key);
      }
    }
  }
}

树的遍历

访问树的所有节点有三种方式:中序、先序、后序。

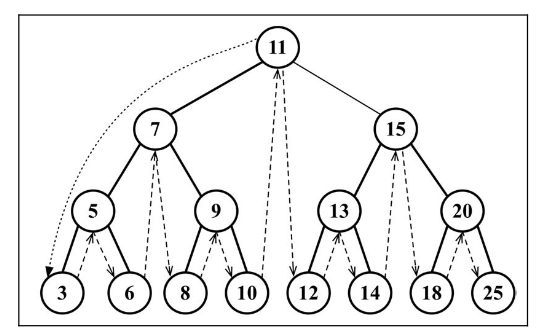
中序遍历

中序遍历是一种以上行顺序访问 BST 所有节点的遍历方式，也就是以从最小到最大的顺序访问所有节点。
中序遍历的一种应用就是对树进行排序操作。

1
2
3
4
5
6
7
8
9
10
11
inOrderTraverse(callback) {
  this.inOrderTraverseNode(this.root, callback)
}

inOrderTraverseNode(node, callback) {
  if(node != null) {
    this.inOrderTraverseNode(node.left, callback)
    callback(node.key)
    this.inOrderTraverseNode(node.right, callback)
  }
}

先序遍历

先序遍历是以优先于后代节点的顺序访问每个节点的。先序遍历的一种应用是打印一个结构化的文档。

1
2
3
4
5
6
7
8
9
10
11
preOrderTraverse(callback) {
  this.preOrderTraverseNode(this.root, callback);
}

preOrderTraverseNode(node, callback) {
  if (node != null) {
    callback(node.key);
    this.preOrderTraverseNode(node.left, callback);
    this.preOrderTraverseNode(node.right, callback);
  }
}

后序遍历

后序遍历则是先访问节点的后代节点，再访问节点本身。后序遍历的一种应用是计算一个目录及其子目录中所有文件所占空间的大小。

1
2
3
4
5
6
7
8
9
10
11
postOrderTraverse(callback) {
  this.postOrderTraverseNode(this.root, callback);
}

postOrderTraverseNode(node, callback) {
  if (node != null) {
    this.postOrderTraverseNode(node.left, callback);
    this.postOrderTraverseNode(node.right, callback);
    callback(node.key);
  }
}

搜索树中的值

在树中，有三种经常执行的搜索类型:

  • 搜索最小值
  • 搜索最大值
  • 搜索特定的值

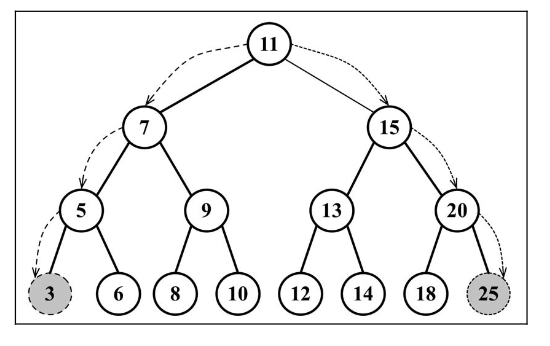
搜索最大值和最小值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
min() {
  return this.minNode(this.root)
}

minNode(node) {
  let current = node;
  while(current != null && current.left != null) {
    current = current.left
  }
  return current
}

max() {
  return this.maxNode(this.root)
}

maxNode(node) {
  let current = node;
  while(current != null && current.right != null) {
    current = current.right
  }
  return current
}

搜索一个特定的值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
search(key) {
  return this.searchNode(this.root, key)
}

searchNode(node, key) {
  if(node == null) {
    return false
  }
  if(this.compareFn(node.key, key) === Compare.LESS_THAN) {
    return this.searchNode(node.left, key)
  } else if(this.compareFn(node.key, key) === Compare.BIGGER_THAN) {
    return this.searchNode(node.right, key)
  } else {
    return true
  }
}

移除一个节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
remove(key) {
  this.root = this.removeNode(this.root, key)
}

removeNode(node, key) {
if(node == null) {
    return false
  }
  if(this.compareFn(node.key, key) === Compare.LESS_THAN) {
    node.left = this.removeNode(node.left, key)
    return node
  } else if(this.compareFn(node.key, key) === Compare.BIGGER_THAN) {
    node.right = this.removeNode(node.right, key)
    return node
  } else {
    // 移除一个叶节点
    if(node.left == null && node.right == null) {
      node = null
      return node
    }

    // 移除有一个左侧或者右侧子节点的节点
    if(node.right == null) {
      node = node.left
      return node
    } else if(node.left == null) {
      node = node.right
      return node
    }

    // 移除有两个子节点的节点
    const aux = this.minNode(node.right)
    node.key = aux.key
    node.right = this.removeNode(node.right, aux.key)
    return node
  }
}

自平衡树

AVL树是一种自平衡二叉搜索树，意思是任何一个节点左右两侧子树的高度之差最多为 1。

Adelson-Velskii-Landi 树(AVL 树)

AVL树是一种自平衡树。添加或移除节点时，AVL 树会尝试保持自平衡。任意一个节点（不论深度）的左子树和右子树高度最多相差1。添加或移除节点时，AVL 树会尽可能尝试转换为完全树。

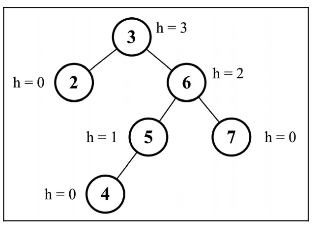
节点的高度和平衡因子

节点的高度：从节点到其任意子节点的边的最大值。如图：

1
2
3
4
5
6
getNodeHeight(node) {
  if(node == null) {
    return -1
  }
  return Math.max(this.getNodeHeight(node.left), this.getNodeHeight(node.right)) + 1
}

计算一个节点的平衡因子并返回其值的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
const BalanceFactor = {
  UNBALANCED_RIGHT: 1,
  SLIGHTLY_UNBALANCED_RIGHT: 2,
  BALANCED: 3,
  SLIGHTLY_UNBALANCED_LEFT: 4,
  UNBALANCED_LEFT: 5
};

getBalanceFactor(node) {
  const heightDifference = this.getNodeHeight(node.left) - this.getNodeHeight(node.right)
  switch(heightDifference) {
    case -2:
      return BalanceFactor.UNBALANCED_RIGHT;
    case -1:
      return BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT;
    case 1:
      return BalanceFactor.SLIGHTLY_UNBALANCED_LEFT;
    case 2:
      return BalanceFactor.UNBALANCED_LEFT;
    default:
      return BalanceFactor.BALANCED;
  }
}

平衡操作——AVL旋转

向 AVL 树插入节点时，可以执行单旋转或双旋转两种平衡操作，分别对应四种场景。

  • 左-左（LL）：向右的单旋转
  • 右-右（RR）：向左的单旋转
  • 左-右（LR）：向右的双旋转（先LL旋转，再RR旋转）
  • 右-左（RL）：向左的双旋转（先RR旋转，再LL旋转）

左-左(LL):向右的单旋转

这种情况出现于节点的左侧子节点的高度大于右侧子节点的高度时，并且左侧子节点也是平衡或左侧较重的，如下图所示: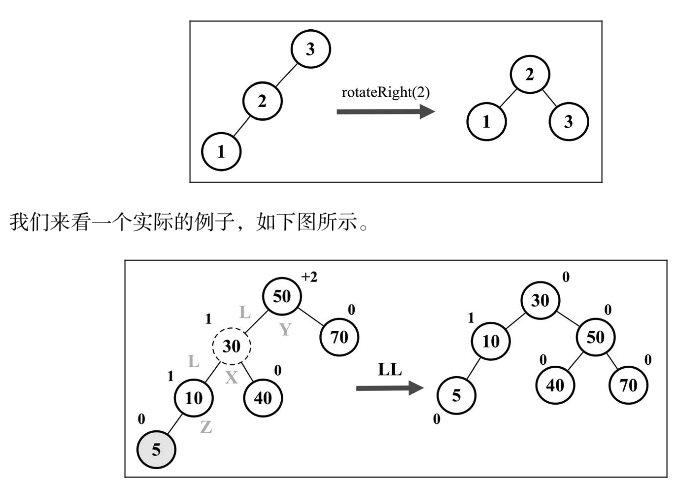

1
2
3
4
5
6
rotationLL(node) {
  const tmp = node.left
  node.left = tmp.right
  tmp.right = node;
  return tmp
}

右-右(RR):向左的单旋转

它出现于右侧子节点的高度大于左侧子节点的高度，并且右侧子节点也是平衡或右侧较重的,如下图所示: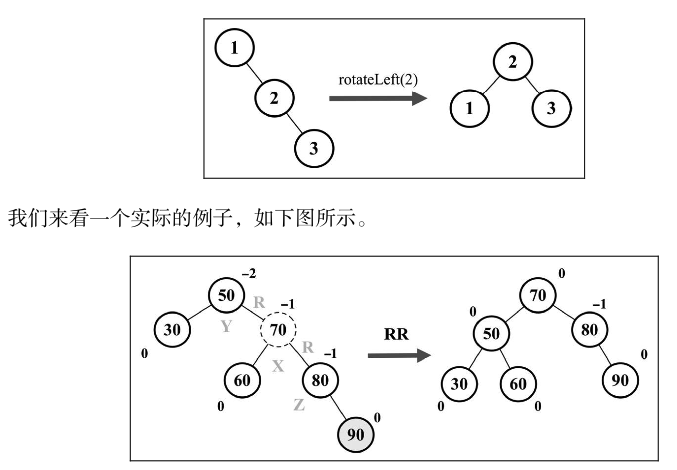

1
2
3
4
5
6
rotationRR(node) {
  const tmp = node.right
  node.right = tmp.left
  tmp.left = node
  return tmp
}

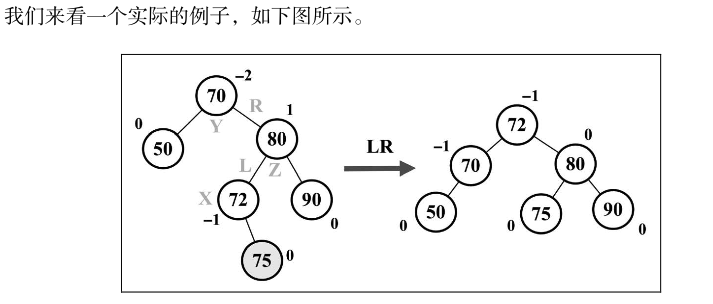
左-右(LR):向右的双旋转

左侧子节点的高度大于右侧子节点的高度，并且左侧子节点右侧较重。在这种情况下，我们可以对左侧子节点进行左旋转来修复，这样会形成左左的情况，然后再对不平衡的节点进行一个右旋转来修复，如下图所示：


基本上，先做一次LL旋转，再做一次RR旋转

1
2
3
4
rotationLR(node) {
  node.right = this.rotationLL(node.right)
  return this.rotationRR(node)
}

右-左(RL):向左的双旋转

右侧子节点的高度大于左侧子节点的高度，并且右侧子节点左侧较重。在这种情况下我们可以对右侧子节点进行右旋转来修复，这样会 形成右-右的情况，然后我们再对不平衡的节点进行一个左旋转来修复，如下图所示。


基本上，先做一次RR旋转，在做一次LL旋转

1
2
3
4
rotationRL(node) {
  node.left = this.rotationRR(node.left)
  return this.rotationLL(node)
}

向AVL树插入节点

插入树后还需验证是否平衡，如果不是，需要进行必要的旋转操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
insert(key) {
  this.root = this.insertNode(this.root, key)
}

insertNode(node, key) {
  // 像在BST树中一样插入节点
  if(node == null) {
    return new Node(key)
  } else if(this.compareFn(key, node.key) === Compare.LESS_THAN) {
    node.left = this.insertNode(node.left, key)
  } else if(this.compareFn(key, node.key) === Compare.BIGGER_THAN) {
    node.right = this.insertNode(node.right, key)
  } else {
    return node // 重复的键
  }

  const balanceFactor = this.getBalanceFactor(node)
  if(balanceFactor === BalanceFactor.UNBALANCED_LEFT) {
    if(this.compareFn(key, node.left.key) === Compare.LESS_THAN) {
      node = this.rotationLL(node)
    } else {
      return this.rotationLR(node)
    }
  }
  if(balanceFactor === BalanceFactor.UNBALANCED_RIGHT) {
    if(this.compareFn(key, node.left.key) === Compare.BIGGER_THAN) {
      node = this.rotationRR(node)
    } else {
      return this.rotationRL(node)
    }
  }
  return node
}

从AVL树中移除节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
removeNode(node, key) {
  node = super.removeNode(node, key);
  if(node == null) {
    return node; //null, 不需要进行平衡
  }

  // 检测是否平衡
  const balanceFactor = this.getBalanceFactor(node)
  if(balanceFactor = BalanceFactor.UNBALANCED_LEFT) {
    const balanceFactorLeft = this.getBalanceFactor(node.left);
    if(balanceFactorLeft === BalanceFactor.BALANCED || balanceFactorLeft === BalanceFactor.SLIGHTLY_UNBALANCED_LEFT) {
      return this.rotationLL(node)
    }
    if(balanceFactorLeft === BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT) {
      return this.rotationLR(node.left)
    }
  }
  if(balanceFactor = BalanceFactor.UNBALANCED_RIGHT) {
    const balanceFactorLeft = this.getBalanceFactor(node.right);
    if(balanceFactorRight === BalanceFactor.BALANCED || balanceFactorRight === BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT) {
      return this.rotationRR(node)
    }
    if(balanceFactorRight === BalanceFactor.SLIGHTLY_UNBALANCED_LEFT) {
      return this.rotationLR(node.right)
    }
  }
  return node
}

红黑树

红黑树也是一个自平衡二叉搜索树。
红黑树适用于多次插入和删除。
在红黑树中，每个节点都遵循以下规则：

  • 每个节点不是红的就黑的
  • 树的根节点树黑的
  • 所有叶节点都是黑的（用NULL引用表示的节点）
  • 如果一个节点是红的，那么它的两个子节点都是黑的
  • 不能有两个相邻的红节点，一个红节点不能有红的父节点或子节点
  • 从给定的节点到它的后代节点（NULL叶节点）的所有路径包含相同数量的黑色节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class RedBlackNode extends Node {
  constructor(key) {
    super(key);
    this.key = key;
    this.color = Colors.RED;
    this.parent = null;
  }

  isRed() {
    return this.color === Colors.RED;
  } 
}

class RedBlackTree extends BinarySearchTree {
  constructor(compareFn = defaultCompare) {
    super(compareFn)
    this.compareFn = compareFn
    this.root = null
  }

  insert(key) {
    if(this.root == null) {
      this.root = new RedBlackNode(key)
      this.root.color = Colors.Black
    } else {
      const newNode = this.insertNode(this.root, key)
      this.fixTreeProperties(newNode)
    }
  }

  insertNode(node, key) {
    if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
      if(node.left == null) {
        node.left = new RedBlackNode(key)
        node.left.parent = node
        return node.left
      } else {
        return this.insertNode(node.left, key)
      }
    } else if(node.right == null) {
      node.right = new RedBlackNode(key)
      node.right.parent = node
      return node.right
    } else {
      return this.insertNode(node.right, key)
    }
  }
}

在插入节点后验证红黑树属性

要验证红黑树是否还是平衡的以及满足它的所有要求，我们需要使用两个概念:

  • 重新填色
  • 旋转

在节点的叔节点颜色为黑时，也就是说仅仅重新填色是不够的，树是不平衡的，那么我们需要进行旋转操作。

  • 左-左(LL):父节点是祖父节点的左侧子节点，节点是父节点的右侧子节点(情形 2A)
  • 左-右(LR):父节点是祖父节点的左侧子节点，节点是父节点的左侧子节点(情形 3A)
  • 右-右(RR):父节点是祖父节点的右侧子节点，节点是父节点的左侧子节点(情形 2B)
  • 右-左(RL):父节点是祖父节点的右侧子节点，节点是父节点的右侧子节点(情形 3B)

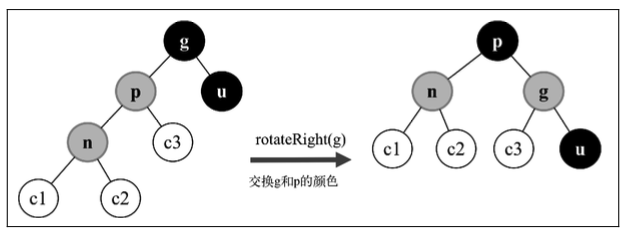
情形2A：

情形2A进行左旋转后会变成情形3A：
情形3A：

情形2B：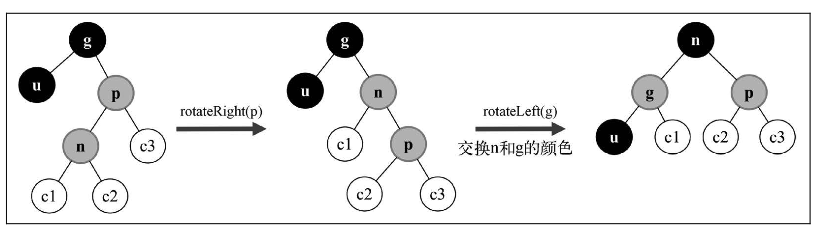

情形3B：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
fixTreeProperties(node) {
  while(node && node.parent && node.parent.color.isRed() && node.color !== Colors.BLACK) {
    let parent = node.parent
    const grandParent = node.parent.parent

    // 情形A:父节点是左侧子节点
    if(grandParent && grandParent.left === parent) {
      const uncle = grandParent.right
      // 情形1A:叔节点也是红色——只需要重新填色
      if(uncle && uncle.color === Colors.RED) {
        grandParent.color = Colors.RED
        parent.color = Colors.Black
        uncle.color = Colors.Black
        node = grandParent
      } else {
        // 情形2A:节点是右侧子节点--左旋转
        if(node === parent.right) {
          this.rorationRR(parent)
          node = parent
          parent = node.parent
        }
        // 情形3A:节点是左侧子节点--右旋转
        this.rotationLL(grandParent)
        parent.color = Colors.BLACK
        grandParent.color = Colors.RED
      }
    } else { // 情形B: 父节点是右侧子节点
      const uncle = grandparent.left
      // 情形1B:叔节点也是红色——只需要重新填色
      if(uncle && uncle.color === Colors.RED) {
        grandParent.color = Colors.RED
        parent.color = Colors.Black
        uncle.color = Colors.Black
        node = grandParent
      } else {
        // 情形2B:节点是右侧子节点--右旋转
        if(node === parent.left) {
          this.rotationLL()
          node = parent
          parent = node.parent
        }
        // 情形3B:节点是左侧子节点--左旋转
        this.rotationRR(grandParent)
        parent.color = Colors.BLACK
        grandParent.color = Colors.RED
        node = parent
      }
    }
  }
  this.root.color = Colors.BLACK
}

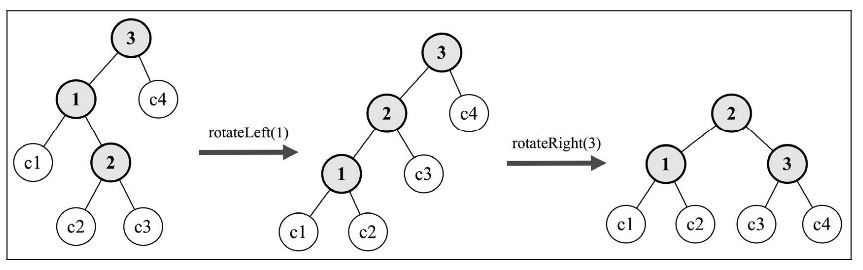
红黑树旋转

在插入算法中，我们只使用了右右旋转和左左旋转。逻辑和 AVL 树是一样，但是，由于我们保存了父节点的引用，需要将引用更新为旋转后的新父节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
rotationLL(node) {
  const tmp = node.left
  node.left = = tmp.right
  if(tmp.right && tmp.right.key) {
    tmp.right.parent = node
  }
  tmp.parent = node.parent
  if(!node.parent) {
    this.root = tmp
  } else {
    if(node === node.parent.left) {
      node.parent.left = tmp
    } else {
      node.parent.right = tmp
    }
  }
  tmp.right = node
  node.parent = tmp
}

rotationRR(node) {
  const tmp = node.right
  node.right = tmp.left
  if(tmp.left && tmp.left.key) {
    tmp.left.parent = node
  }
  tmp.parent = node.parent
  if(!node.parent) {
    this.root = tmp
  } else {
    if(node === node.parent.left) {
      node.parent.left = tmp
    } else {
      node.parent.right = tmp
    }
  }
  tmp.left = node
  node.parent = tmp
}
liborn wechat
欢迎您扫一扫上面的微信二维码，订阅我的公众号！